You are given the root of a binary tree with unique values, and an integer start. At minute 0, an infection starts from the node with value start.
Each minute, a node becomes infected if:
- The node is currently uninfected.
- The node is adjacent to an infected node.
Return the number of minutes needed for the entire tree to be infected.
Example 1:
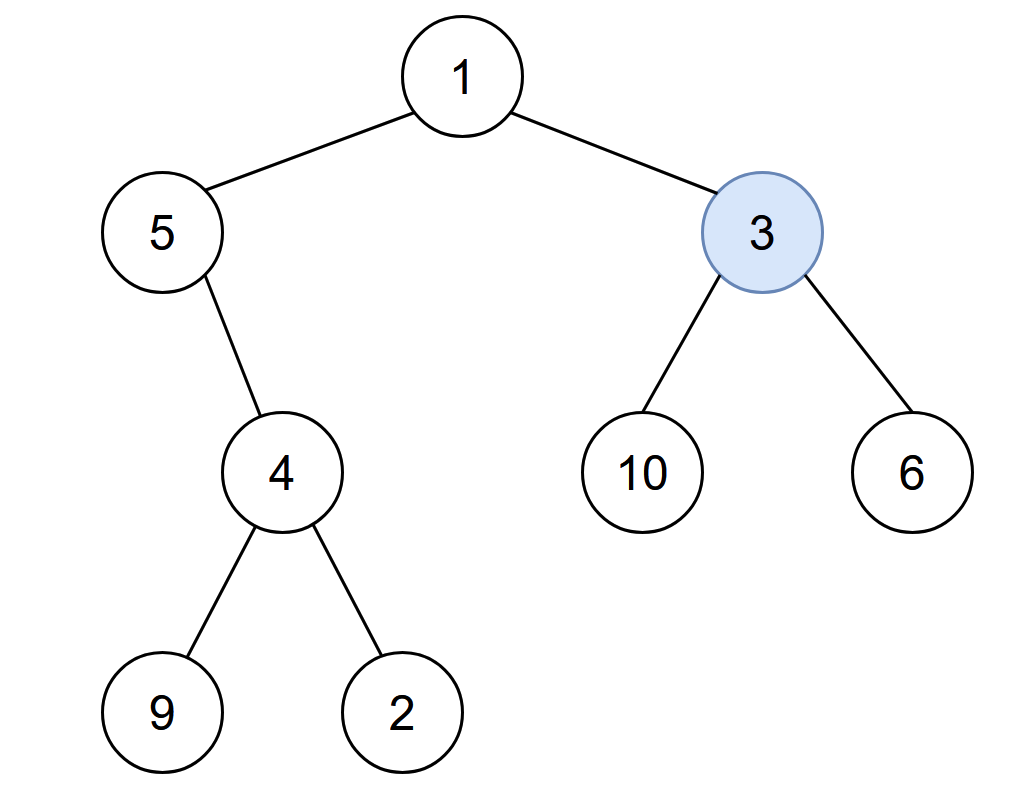
Input: root = [1,5,3,null,4,10,6,9,2], start = 3
Output: 4
Explanation: The following nodes are infected during:
- Minute 0: Node 3
- Minute 1: Nodes 1, 10 and 6
- Minute 2: Node 5
- Minute 3: Node 4
- Minute 4: Nodes 9 and 2
It takes 4 minutes for the whole tree to be infected so we return 4.
Example 2:

Input: root = [1], start = 1
Output: 0
Explanation: At minute 0, the only node in the tree is infected so we return 0.
Constraints:
- The number of nodes in the tree is in the range
[1, 105].
1 <= Node.val <= 105- Each node has a unique value.
- A node with a value of
start exists in the tree.
## Solution(Python)
```Python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
from collections import defaultdict, deque
class Solution:
def amountOfTime(self, root: Optional[TreeNode], start: int) -> int:
return self.onepass(root, start)
# TIme complexity: O(n)
# Space complexiy: O(n)
def twopass(self, root: Optional[TreeNode], start: int) -> int:
# 1 build the graph from tree make connectionfrom node -> parents
graph = defaultdict(list)
def buidlGraph(cur, parent):
if cur is not None and parent is not None:
graph[cur.val].append(parent.val)
graph[parent.val].append(cur.val)
if cur.left is not None:
buidlGraph(cur.left, cur)
if cur.right is not None:
buidlGraph(cur.right, cur)
buidlGraph(root, None)
# 2 run dfs from the start node and track the maximum length by a max _length variable
max_len = 0
queue = deque([(start, 0)])
visited = set([start])
while len(queue) > 0:
node, distance = queue.popleft()
if distance > max_len:
max_len = distance
for neighbour in graph[node]:
if neighbour not in visited:
visited.add(neighbour)
queue.append((neighbour, distance+1))
return max_len
# TIme complexity: O(n)
# Space complexiy: O(n)
def onepass(self, root: Optional[TreeNode], start: int) -> int:
max_distance = 0
def traverse(root, start):
nonlocal max_distance
depth = 0
if root is None:
return depth
left_depth = traverse(root.left, start)
right_depth = traverse(root.right, start)
if root.val == start:
max_distance = max(left_depth, right_depth)
depth = -1
elif left_depth >= 0 and right_depth >= 0:
depth = max(left_depth, right_depth) + 1
else:
distance = abs(left_depth) + abs(right_depth)
max_distance = max(max_distance, distance)
depth = min(left_depth, right_depth) - 1
return depth
traverse(root,start)
return max_distance
```
