# 473-matchsticks-to-square


Try it on <a href='https://leetcode.com/problems/473-matchsticks-to-square'>leetcode</a>

## Description
<div class="description">
<div><p>You are given an integer array <code>matchsticks</code> where <code>matchsticks[i]</code> is the length of the <code>i<sup>th</sup></code> matchstick. You want to use <strong>all the matchsticks</strong> to make one square. You <strong>should not break</strong> any stick, but you can link them up, and each matchstick must be used <strong>exactly one time</strong>.</p>

<p>Return <code>true</code> if you can make this square and <code>false</code> otherwise.</p>

<p>&nbsp;</p>
<p><strong>Example 1:</strong></p>
<img alt="" src="https://assets.leetcode.com/uploads/2021/04/09/matchsticks1-grid.jpg" style="width: 253px; height: 253px;">
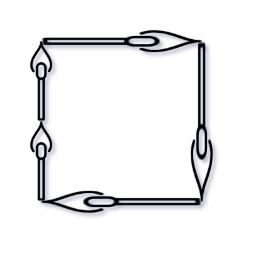
<pre><strong>Input:</strong> matchsticks = [1,1,2,2,2]
<strong>Output:</strong> true
<strong>Explanation:</strong> You can form a square with length 2, one side of the square came two sticks with length 1.
</pre>

<p><strong>Example 2:</strong></p>

<pre><strong>Input:</strong> matchsticks = [3,3,3,3,4]
<strong>Output:</strong> false
<strong>Explanation:</strong> You cannot find a way to form a square with all the matchsticks.
</pre>

<p>&nbsp;</p>
<p><strong>Constraints:</strong></p>

<ul>
	<li><code>1 &lt;= matchsticks.length &lt;= 15</code></li>
	<li><code>1 &lt;= matchsticks[i] &lt;= 10<sup>8</sup></code></li>
</ul>
</div>
</div>

## Solution(Python)
```Python
class Solution:
    def makesquare(self, matchsticks: List[int]) -> bool:
        return self.dp(matchsticks)

    """
    Time Complexity: O(4^n)
    Space Complexity: O(n)
    """

    def dfs(self, matchsticks: List[int]) -> bool:
        if not matchsticks:
            return False

        length = sum(matchsticks) // 4

        if sum(matchsticks) / 4 != length:
            return False

        matchsticks.sort(reverse=True)
        sides = [0] * 4

        def backtrack(i):
            if i == len(matchsticks):
                return True

            for j in range(4):
                if sides[j] + matchsticks[i] <= length:
                    sides[j] += matchsticks[i]
                    if backtrack(i + 1):
                        return True
                    sides[j] -= matchsticks[i]

            return False

        return backtrack(0)

    """
    Time Complexity: O(n*2^n)
    Space Complexity: O(n+2^n)
    """

    def dp(self, matchsticks: List[int]) -> bool:
        if not matchsticks:
            return False

        lth = len(matchsticks)

        perimeter = sum(matchsticks)
        side = perimeter // 4

        if side * 4 != perimeter:
            return False

        dp = {}

        def recur(mask, sidesfilledsofar):
            total = 0

            for i in range(lth - 1, -1, -1):
                if not (mask & (1 << i)):
                    total += matchsticks[lth - 1 - i]

            if total > 0 and total % side == 0:
                sidesfilledsofar += 1

            if sidesfilledsofar == 3:
                return True

            if (mask, sidesfilledsofar) in dp:
                return dp[(mask, sidesfilledsofar)]

            ans = False

            remainingspace = side * (int(total / side) + 1) - total

            for i in range(lth - 1, -1, -1):
                if matchsticks[lth - 1 - i] <= remainingspace and mask & (1 << i):
                    if recur(mask ^ (1 << i), sidesfilledsofar):
                        ans = True
                        break
            dp[(mask, sidesfilledsofar)] = ans
            return ans

        return recur((1 << lth) - 1, 0)

```