Given an array of integers heights representing the histogram's bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.
Example 1:
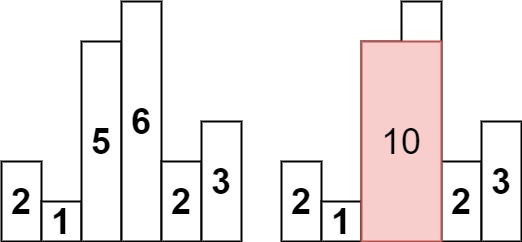
Input: heights = [2,1,5,6,2,3] Output: 10 Explanation: The above is a histogram where width of each bar is 1. The largest rectangle is shown in the red area, which has an area = 10 units.
Example 2:
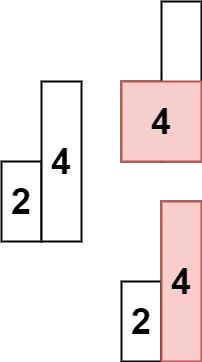
Input: heights = [2,4] Output: 4
Constraints:
1 <= heights.length <= 1050 <= heights[i] <= 104