Given the root of a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.
Example 1:
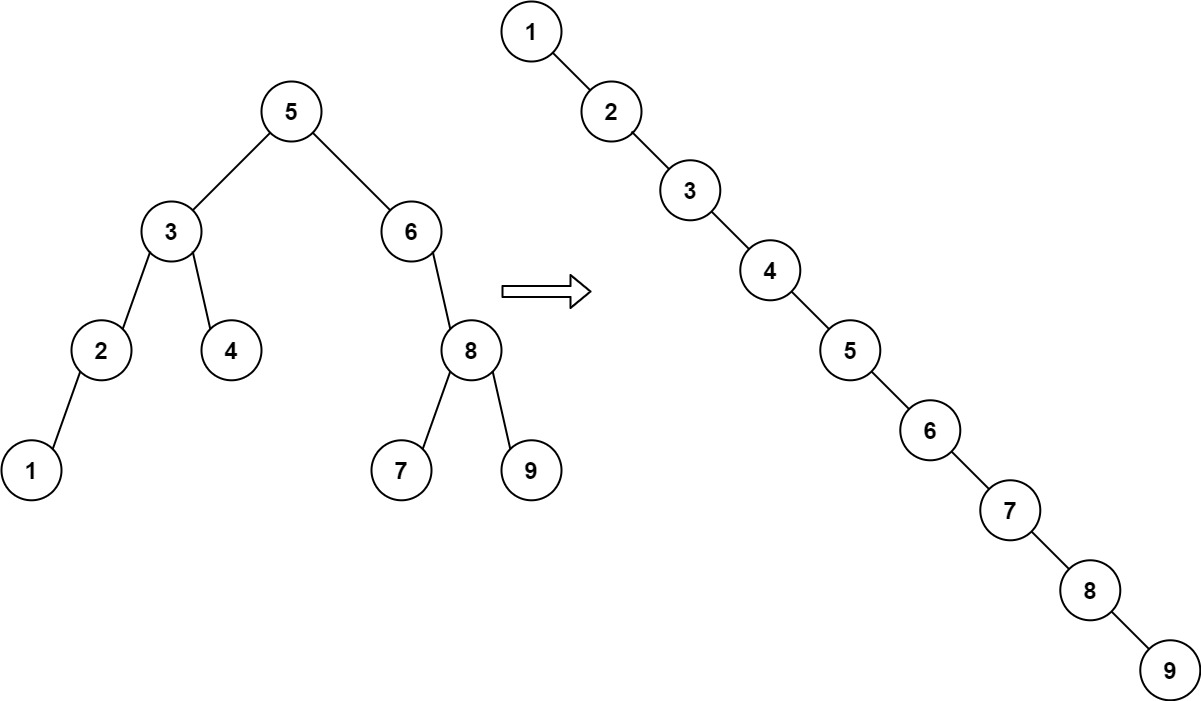
Input: root = [5,3,6,2,4,null,8,1,null,null,null,7,9] Output: [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]
Example 2:
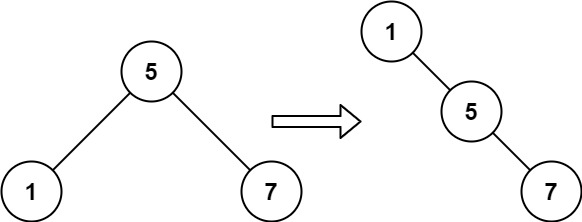
Input: root = [5,1,7] Output: [1,null,5,null,7]
Constraints:
- The number of nodes in the given tree will be in the range
[1, 100]. 0 <= Node.val <= 1000