1022-sum-of-root-to-leaf-binary-numbers

Try it on leetcode

Description

You are given the root of a binary tree where each node has a value 0 or 1. Each root-to-leaf path represents a binary number starting with the most significant bit.

• For example, if the path is 0 -> 1 -> 1 -> 0 -> 1, then this could represent 01101 in binary, which is 13.

For all leaves in the tree, consider the numbers represented by the path from the root to that leaf. Return the sum of these numbers.

The test cases are generated so that the answer fits in a 32-bits integer.

 

Example 1:

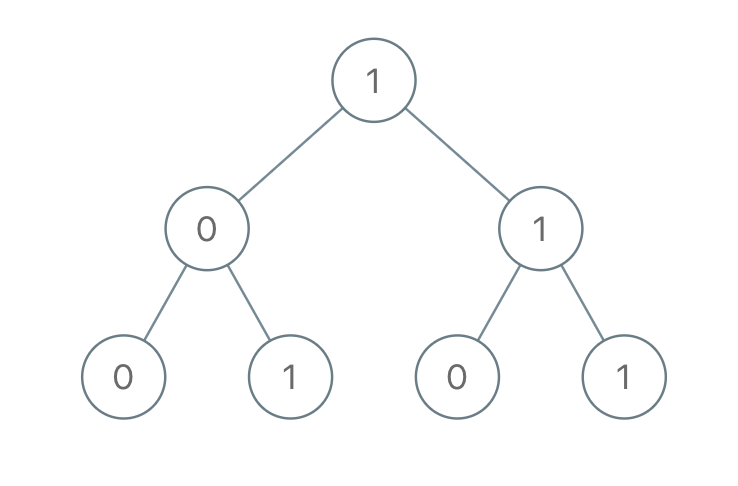
Input: root = [1,0,1,0,1,0,1]
Output: 22
Explanation: (100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22

Example 2:

Input: root = [0]
Output: 0

 

Constraints:

• The number of nodes in the tree is in the range [1, 1000].
• Node.val is 0 or 1.

Solution(Python)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def sumRootToLeaf(self, root: Optional[TreeNode]) -> int:
        return self.preorderMorrisTraversal(root)

    # Time Complexity: O(n)
    # Space Complexity: O(H)
    def preorderIterativeTraversal(self, root) -> int:
        res = 0
        s = []
        s.append((root, 0))

        while s:
            node, curr = s.pop()
            if node is not None:
                curr = (curr << 1) | node.val

                if node.left is None and node.right is None:
                    res += curr
                else:
                    s.append((node.right, curr))
                    s.append((node.left, curr))

        return res

    # Time Complexity: O(n)
    # Space Complexity: O(H)
    def preorderRecursiveTraversal(self, root) -> int:
        res = 0

        def dfs(node, cur):
            nonlocal res
            cur = (cur << 1) | node.val

            if node.left is None and node.right is None:
                res += cur
            if node.right is not None:
                dfs(node.right, cur)
            if node.left is not None:
                dfs(node.left, cur)

        dfs(root, 0)
        return res

    # Time Complexity: O(n)
    # Space Complexity: O(1)
    def preorderMorrisTraversal(self, root) -> int:
        res = 0

        node = root
        cur = 0

        while node:
            if node.left:
                pred = node.left
                steps = 1
                while pred.right and pred.right is not node:
                    pred = pred.right
                    steps += 1

                if pred.right is None:
                    cur = (cur << 1) | node.val
                    pred.right = node
                    node = node.left
                else:
                    if pred.left is None:
                        res += cur
                    for _ in range(steps):
                        cur >>= 1
                    pred.right = None
                    node = node.right
            else:
                cur = (cur << 1) | node.val
                if node.right is None:
                    res += cur
                node = node.right
        return res