1091-shortest-path-in-binary-matrix¶

Description¶

Given an n x n binary matrix grid, return the length of the shortest clear path in the matrix. If there is no clear path, return -1.

A clear path in a binary matrix is a path from the top-left cell (i.e., (0, 0)) to the bottom-right cell (i.e., (n - 1, n - 1)) such that:

All the visited cells of the path are 0.
All the adjacent cells of the path are 8-directionally connected (i.e., they are different and they share an edge or a corner).

The length of a clear path is the number of visited cells of this path.

Example 1:

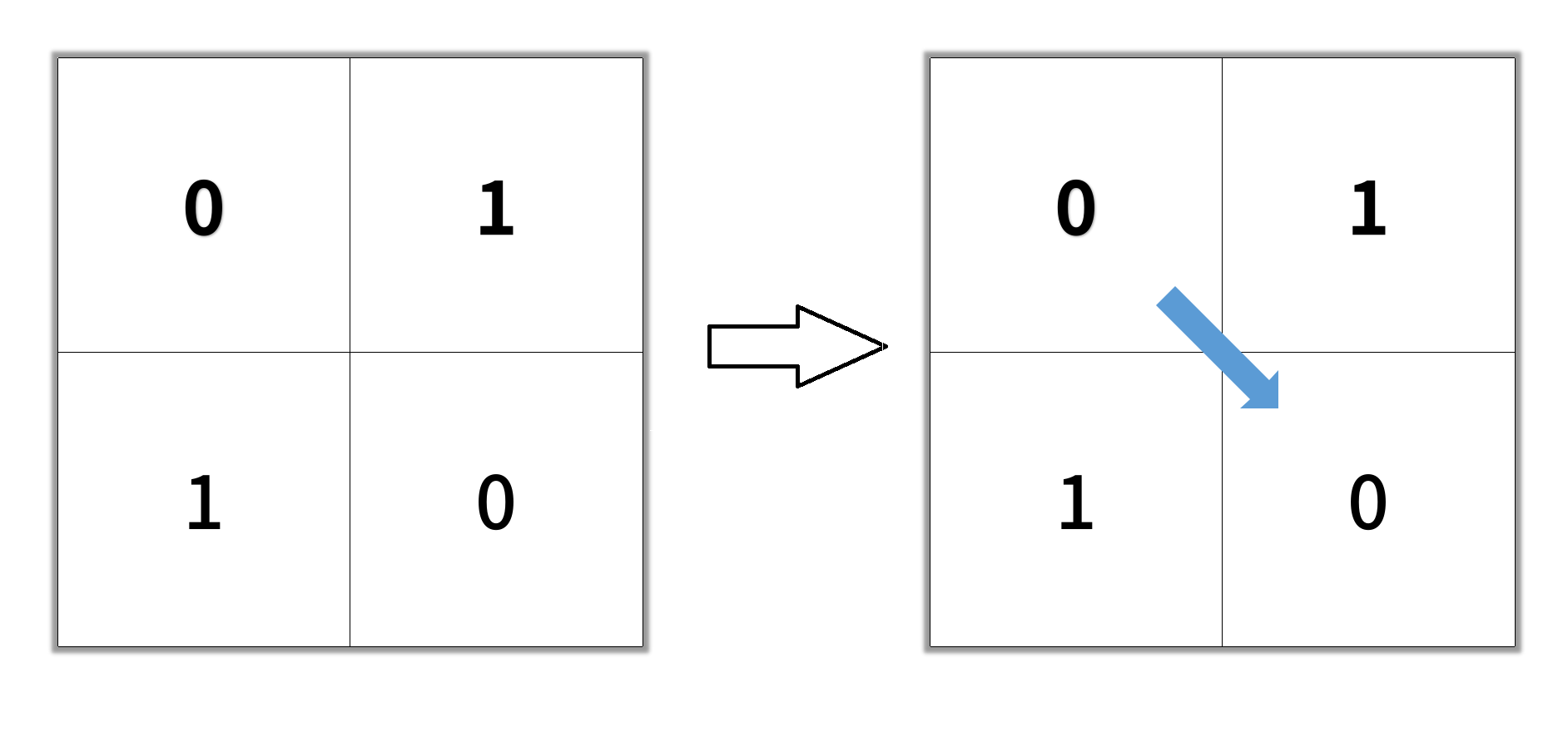
Input: grid = [[0,1],[1,0]]
Output: 2

Example 2:

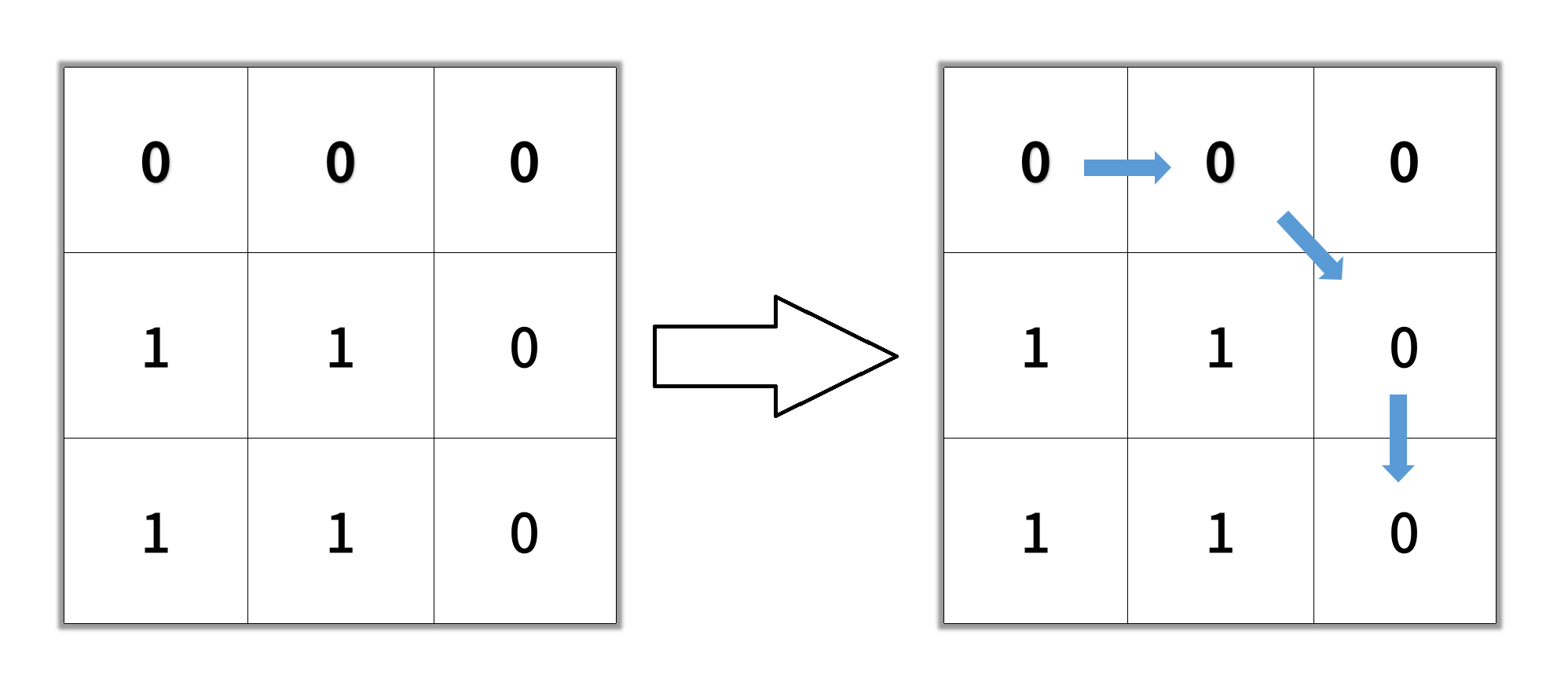
Input: grid = [[0,0,0],[1,1,0],[1,1,0]]
Output: 4

Example 3:

Input: grid = [[1,0,0],[1,1,0],[1,1,0]]
Output: -1

Constraints:

n == grid.length
n == grid[i].length
1 <= n <= 100
grid[i][j] is 0 or 1

Solution(Python)¶

class Solution:
    def shortestPathBinaryMatrix(self, grid: List[List[int]]) -> int:
        return self.doublebfs(grid)

    # Time Complexity: O(n^2)
    # Space Complexity: O(n^2)
    def bfs(self, grid: List[List[int]]) -> int:
        n = len(grid)
        neighs = [(-1, -1), (-1, 0), (-1, 1), (0, -1),
                  (0, 1), (1, -1), (1, 0), (1, 1)]
        if grid[0][0]:
            return -1

        queue = deque([(1, 0, 0)])
        visited = set()
        visited.add((0, 0))

        while queue:
            dist, x, y = queue.popleft()

            if x == n - 1 and y == n - 1:
                return dist

            for dx, dy in neighs:
                negh_x, negh_y = x + dx, y + dy
                if (
                    -1 < negh_x < n
                    and -1 < negh_y < n
                    and not grid[negh_x][negh_y]
                    and (negh_x, negh_y) not in visited
                ):
                    visited.add((negh_x, negh_y))
                    queue.append((dist + 1, negh_x, negh_y))

        return -1

    # Time Complexity: O(n^2)
    # Space Complexity: O(n^2)
    def doublebfs(self, grid: List[List[int]]) -> int:
        n = len(grid)
        neighs = [(-1, -1), (-1, 0), (-1, 1), (0, -1),
                  (0, 1), (1, -1), (1, 0), (1, 1)]

        if grid[0][0] or grid[n - 1][n - 1]:
            return -1

        if n == 1:
            return 1

        queue1 = deque([(1, 0, 0)])
        queue2 = deque([(1, n - 1, n - 1)])

        visited1 = defaultdict(lambda: 0)
        visited2 = defaultdict(lambda: 0)

        visited1[(0, 0)] = 1
        visited2[(n - 1, n - 1)] = 1

        while queue1 and queue2:
            if queue1:
                dist, x, y = queue1.popleft()

                if (x, y) in visited2:
                    return dist + visited2[(x, y)] - 1

                for dx, dy in neighs:
                    negh_x, negh_y = x + dx, y + dy
                    if (
                        -1 < negh_x < n
                        and -1 < negh_y < n
                        and not grid[negh_x][negh_y]
                        and (negh_x, negh_y) not in visited1
                    ):
                        visited1[(negh_x, negh_y)] = dist + 1
                        queue1.append((dist + 1, negh_x, negh_y))

            if queue2:
                dist, x, y = queue2.popleft()

                if (x, y) in visited1:
                    return dist + visited1[(x, y)] - 1

                for dx, dy in neighs:
                    negh_x, negh_y = x + dx, y + dy
                    if (
                        -1 < negh_x < n
                        and -1 < negh_y < n
                        and not grid[negh_x][negh_y]
                        and (negh_x, negh_y) not in visited2
                    ):
                        visited2[(negh_x, negh_y)] = dist + 1
                        queue2.append((dist + 1, negh_x, negh_y))

        return -1