1192-critical-connections-in-a-network¶

Description¶

There are n servers numbered from 0 to n - 1 connected by undirected server-to-server connections forming a network where connections[i] = [a_i, b_i] represents a connection between servers a_i and b_i. Any server can reach other servers directly or indirectly through the network.

A critical connection is a connection that, if removed, will make some servers unable to reach some other server.

Return all critical connections in the network in any order.

Example 1:

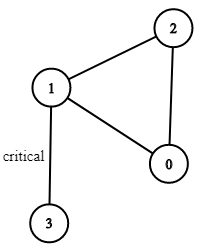
Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]
Output: [[1,3]]
Explanation: [[3,1]] is also accepted.

Example 2:

Input: n = 2, connections = [[0,1]]
Output: [[0,1]]

Constraints:

2 <= n <= 10⁵
n - 1 <= connections.length <= 10⁵
0 <= a_i, b_i <= n - 1
a_i != b_i
There are no repeated connections.

Solution(Python)¶

class Solution:
    def criticalConnections(
        self, n: int, connections: List[List[int]]
    ) -> List[List[int]]:
        return self.optmial(n, connections)

    # Time Complexity: O(E*(V+E))
    # Space Complexity: O(V+E)
    def bruteforce(self, n: int, connections: List[List[int]]) -> List[List[int]]:
        # create graph adj list
        adjList = defaultdict(set)

        for x, y in connections:
            adjList[x].add(y)
            adjList[y].add(x)

        res = []

        # initial number of connected components
        total_com = 0
        visited = [False] * n
        for i in range(n):
            for j in range(n):
                if visited[i] == False and i != j:
                    total_com += 1
                    self.dfs(adjList, i, visited)

        #   remove each E and see if graph remains connected
        for x, y in connections:
            visited = [False] * n

            adjList[x].remove(y)
            adjList[y].remove(x)
            cur_comp = 0

            for i in range(n):
                if visited[i] == False:
                    cur_comp += 1
                    self.dfs(adjList, i, visited)

            # if removal of E increases number of connected compponents then it's a bridge
            if cur_comp > total_com:
                res.append([x, y])

            adjList[x].add(y)
            adjList[y].add(x)
        return res

    # Time Complexity: O((V+E))
    # Space Complexity: O(V+E)
    def dfs(self, adjList, i, visited):
        if visited[i]:
            return
        visited[i] = True
        for j in adjList[i]:
            if not visited[j]:
                self.dfs(adjList, j, visited)

    # Time Complexity: O(V+E)
    # Space Complexity: O(V+E)
    def optmial(self, n: int, connections: List[List[int]]) -> List[List[int]]:
        self.low = [0] * n
        self.disc = [0] * n
        self.res = []
        self.time = 1

        self.adjList = defaultdict(set)

        for x, y in connections:
            self.adjList[x].add(y)
            self.adjList[y].add(x)

        for u in range(n):
            if not self.disc[u]:
                self.optimal_df_util(u, u)

        return self.res

    def optimal_df_util(self, u, p):
        self.time += 1
        self.low[u] = self.disc[u] = self.time

        for v in self.adjList[u]:
            if v == p:
                continue

            if not self.disc[v]:
                self.optimal_df_util(v, u)
                if self.disc[u] < self.low[v]:
                    self.res.append([u, v])
                self.low[u] = min(self.low[u], self.low[v])
            else:
                self.low[u] = min(self.low[u], self.disc[v])