1302-deepest-leaves-sum

Try it on leetcode

Description

Given the 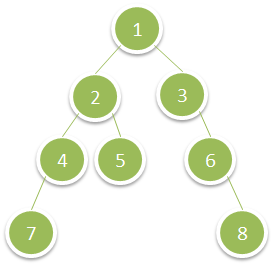root of a binary tree, return the sum of values of its deepest leaves.

 

Example 1:

Input: root = [1,2,3,4,5,null,6,7,null,null,null,null,8]
Output: 15

Example 2:

Input: root = [6,7,8,2,7,1,3,9,null,1,4,null,null,null,5]
Output: 19

 

Constraints:

• The number of nodes in the tree is in the range [1, 104].
• 1 <= Node.val <= 100

Solution(Python)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def deepestLeavesSum(self, root: Optional[TreeNode]) -> int:
        return self.morristraversal(root)

    # Time Complexity: O(n)
    # Space Complexity: O(h)
    def dfs(self, root: Optional[TreeNode]) -> int:
        def lendfs(node):
            if node:
                left = lendfs(node.left)
                right = lendfs(node.right)
                return max(left, right) + 1
            return 0

        length = lendfs(root)
        maxsum = 0

        def calcSum(node, depth):
            nonlocal maxsum
            if not node:
                return
            if depth == 1 and not node.left and not node.right:
                maxsum += node.val

            calcSum(node.left, depth - 1)
            calcSum(node.right, depth - 1)

        calcSum(root, length)
        return maxsum

    # Time Complexity: O(n)
    # Space Complexity: O(h)
    def bfs(self, root: Optional[TreeNode]) -> int:
        q = deque([root])
        cursum = 0

        while q:
            cursum = 0
            qsize = len(q)
            for i in range(qsize):
                p = q.popleft()
                cursum += p.val
                if p.left:
                    q.append(p.left)
                if p.right:
                    q.append(p.right)
        return cursum

    # Time Complexity: O(n)
    # Space Complexity: O(h)
    def singledfs(self, root: Optional[TreeNode]) -> int:
        maxsum = 0
        maxlevel = 0

        def dfs(node, level):
            nonlocal maxsum, maxlevel
            if not node:
                return

            if level > maxlevel:
                maxsum = node.val
                maxlevel = level
            elif level == maxlevel:
                maxsum += node.val

            dfs(node.left, level + 1)
            dfs(node.right, level + 1)

        dfs(root, 0)
        return maxsum

    # Time Complexity: O(n)
    # Space Complexity: O(1)
    def morristraversal(self, root: Optional[TreeNode]) -> int:
        def morris(node):
            depth = 0
            while node:
                if not node.left:
                    yield node.val, depth
                    node = node.right
                    depth += 1
                else:
                    prev = node.left
                    down = 1
                    while prev.right not in (None, node):
                        prev = prev.right
                        down += 1
                    if prev.right:
                        prev.right = None
                        depth -= down + 1
                        yield node.val, depth
                        node = node.right
                        depth += 1
                    else:
                        prev.right = node
                        node = node.left
                        depth += 1

        maxDepth = max(depth for _, depth in morris(root))
        return sum(val for val, depth in morris(root) if depth == maxDepth)