1463-cherry-pickup-ii¶
Try it on leetcode
Description¶
You are given a rows x cols matrix grid representing a field of cherries where grid[i][j] represents the number of cherries that you can collect from the (i, j) cell.
You have two robots that can collect cherries for you:
- Robot #1 is located at the top-left corner
(0, 0), and - Robot #2 is located at the top-right corner
(0, cols - 1).
Return the maximum number of cherries collection using both robots by following the rules below:
- From a cell
(i, j), robots can move to cell(i + 1, j - 1),(i + 1, j), or(i + 1, j + 1). - When any robot passes through a cell, It picks up all cherries, and the cell becomes an empty cell.
- When both robots stay in the same cell, only one takes the cherries.
- Both robots cannot move outside of the grid at any moment.
- Both robots should reach the bottom row in
grid.
Example 1:
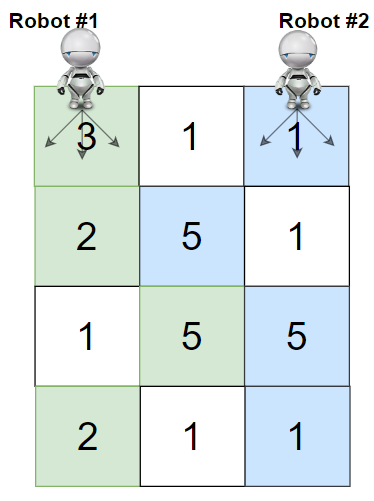
Input: grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]] Output: 24 Explanation: Path of robot #1 and #2 are described in color green and blue respectively. Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12. Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12. Total of cherries: 12 + 12 = 24.
Example 2:
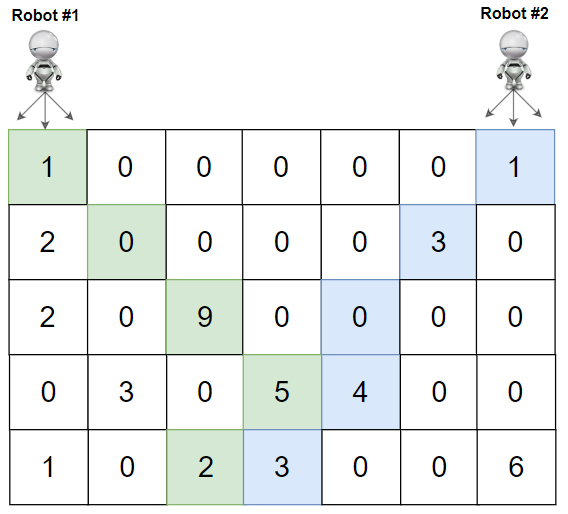
Input: grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]] Output: 28 Explanation: Path of robot #1 and #2 are described in color green and blue respectively. Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17. Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11. Total of cherries: 17 + 11 = 28.
Constraints:
rows == grid.lengthcols == grid[i].length2 <= rows, cols <= 700 <= grid[i][j] <= 100
Solution(Python)¶
# @Problem
# Given matrix of values and the two robots (0,0) and (0,col-j)
# Return max number of cherries with condition
# *from i,j ,valid moves (i+1,j-1),(i+1,j)and(i+1,j+1)
# *when robot sweeps ,matrix[i][j] = 0
# *when two robots in the cells only one cantake it
# *No outside movements
# *Both Robots should reach bottom row
#
# @Input: 2d Matrix
# @output: maximum number of cherries value
#
# @Simple Example:
# 1. grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]]
# Robot 1: 3+2+5+2 = 12
# Robot 2: 1+5+5+1 = 12
# Total = 24
#
# 2. grid =[[1,0,0,0,0,0,1],
# [2,0,0,0,0,3,0]
# [2,0,9,0,0,0,0],
# [0,3,0,5,4,0,0],
# [1,0,2,3,0,0,6]]
# Robot1: 1+0+9+5+2 = 17
# Robot2: 1+3+0+4+3 = 11
# Total = 28
#
# @constraints:
# rows == grid.length
# cols == grid[i].length
# 2 <= rows, cols <= 70
# 0 <= grid[i][j] <= 100
#
#
# @Solution:
# 1.Recursive with DP cache:
# we can construct recursive solution by considering the state
# with robots on the same row.If we use different rows then
# solution may not be optmial.since choice of path 1 influences
# the path 2 which give rises to number of recursive calls
# in cosmic levels. we will keep it simple with moving the robots
# simultaneously by making optimal choices from previous moves
#
# So Dp state will be at (row,Robot1,Robot2) denoting maximum cherries
# if robots at (row,Robot1) and (row,Robot2)
# Base case when Robots reaches the bottom
# at index (row,Robot1,Robot2) each robot can choose three positions
# then two robots can make 3*3 possible moves simultaneuously
# 2.Bottom Up Dp:
# state: p[row][R1][R2]
# Base case: row = row-1 iterarte from bottom
# Recursive case:
# dp[row][R1][R2] += cur_val + max(dp(row+1 for all nine possible values))
#
#
# Soluiton state: dp[0][0][rows]
#
# Time Complexity: O(mn^2)
# Space Complexity: O(mn^2)
class Solution:
def cherryPickup(self, grid: List[List[int]]) -> int:
rows = len(grid)
cols = len(grid[0])
dp = [[[0] * cols for _ in range(cols)] for _ in range(rows)]
# since dp state depends on dp+1 work on way up
for row in reversed(range(rows)):
for R1 in range(cols):
for R2 in range(cols):
res = grid[row][R1]
res += grid[row][R2] if R1 != R2 else 0
if row != rows - 1:
res += max(
dp[row + 1][newR1][newR2]
for newR1 in [R1, R1 + 1, R1 - 1]
for newR2 in [R2, R2 + 1, R2 - 1]
if 0 <= newR1 < cols and 0 <= newR2 < cols
)
dp[row][R1][R2] = res
return dp[0][0][cols - 1]