240-search-a-2d-matrix-ii

Try it on leetcode

Description

Write an efficient algorithm that searches for a target value in an m x n integer matrix. The matrix has the following properties:

• Integers in each row are sorted in ascending from left to right.
• Integers in each column are sorted in ascending from top to bottom.

 

Example 1:

Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output: true

Example 2:

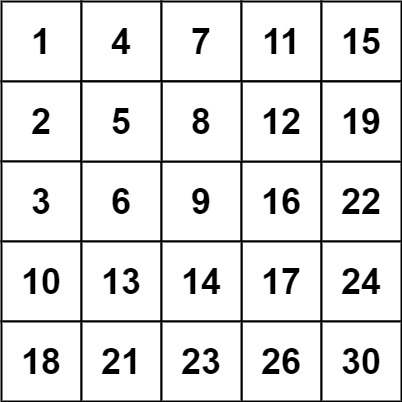
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output: false

 

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= n, m <= 300
• -109 <= matrix[i][j] <= 109
• All the integers in each row are sorted in ascending order.
• All the integers in each column are sorted in ascending order.
• -109 <= target <= 109

Solution(Python)

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        return self.linearSearch(matrix, target)

    # Time Complexity: O(MN)
    # Space Complexity: O(1)
    def bruteforce(self, matrix: List[List[int]], target: int) -> bool:
        m, n = len(matrix), len(matrix[0])

        for i in range(m):
            for j in range(n):
                if matrix[i][j] == target:
                    return True
        return False

    # Time Complexity: O(M+N)
    # Space Complexity: O(1)
    def linearSearch(self, matrix: List[List[int]], target: int) -> bool:
        m, n = len(matrix), len(matrix[0])
        i, j = 0, n - 1

        while i <= m - 1 and j >= 0:
            curr = matrix[i][j]

            if target == curr:
                return True

            if target > curr:
                i += 1
            else:
                j -= 1

        return False