695-max-area-of-island¶

Description¶

You are given an m x n binary matrix grid. An island is a group of 1's (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.

The area of an island is the number of cells with a value 1 in the island.

Return the maximum area of an island in grid. If there is no island, return 0.

Example 1:

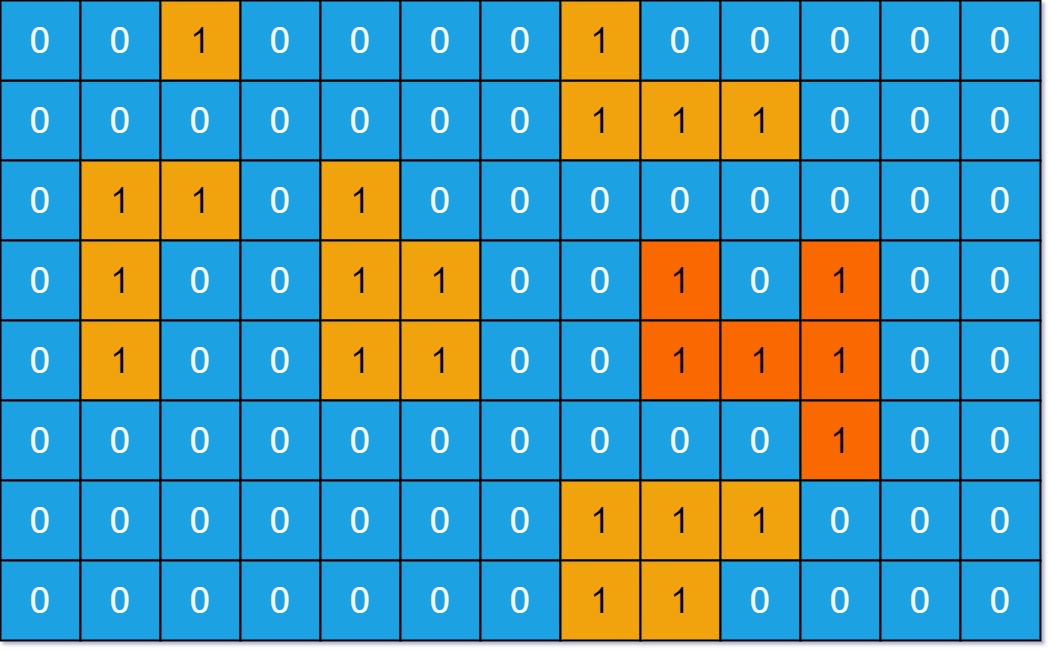
Input: grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
Output: 6
Explanation: The answer is not 11, because the island must be connected 4-directionally.

Example 2:

Input: grid = [[0,0,0,0,0,0,0,0]]
Output: 0

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 50
grid[i][j] is either 0 or 1.

Solution(Python)¶

class Solution:
    def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
        return self.dfs(grid)
        
    # Time Compleixty: O(m*n)
    # Space complexity: O(m*n)
    def dfs(self, grid: List[List[int]]) -> int:
        seen = set()
        def area(r, c):
            if not (0 <= r < len(grid) and 0 <= c < len(grid[0])
                    and (r, c) not in seen and grid[r][c]):
                return 0
            seen.add((r, c))
            return (1 + area(r+1, c) + area(r-1, c) +
                    area(r, c-1) + area(r, c+1))

        return max(area(r, c)
                   for r in range(len(grid))
                   for c in range(len(grid[0])))
    
    # Time Compleixty: O(n^2)
    # Space complexity: O(n^2)
    def betterbruteforce(self, grid: List[List[int]]) -> int:
        m,n = len(grid), len(grid[0])if grid[0] else 0 
        if not n or not m:
            return 0
        max_area = 0
        dirs = [(1,0), (-1,0), (0,-1), (0,1)]
        
        def dfs(x,y, visited):
            res = 1
            
            for dx, dy in dirs:
                x1,y1 = x+dx, y+dy
                if 0 <= x1 <= m-1 and 0 <= y1 <= n-1 and (x1,y1) not in visited and grid[i][j]:
                    visited.add((x1,y1))
                    res += dfs(x1,y1, visited)
                else:
                    continue
            return res
        visited = set()
        for i in range(m):
            for j in range(n):
                if grid[i][j] and (i,j) not in visited:
                    visited.add((i,j))
                    max_area = max(max_area, dfs(i,j, visited))

        return max_area