897-increasing-order-search-tree

Try it on leetcode

Description

Given the root of a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.

 

Example 1:

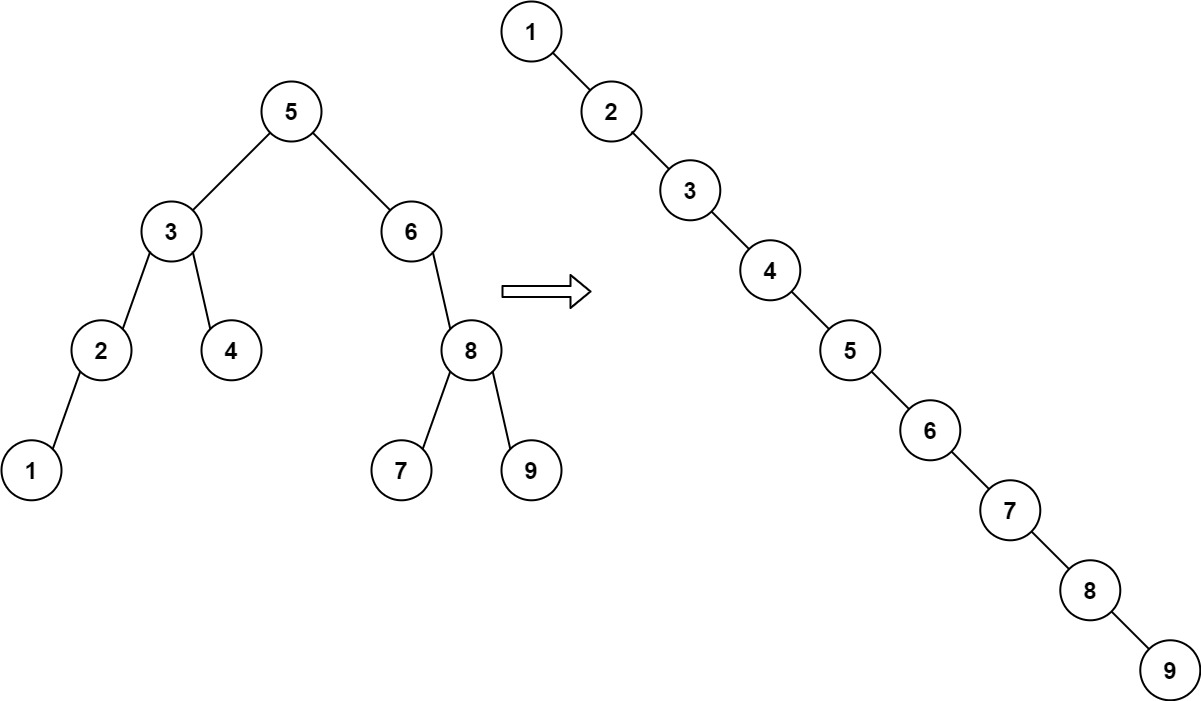
Input: root = [5,3,6,2,4,null,8,1,null,null,null,7,9]
Output: [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]

Example 2:

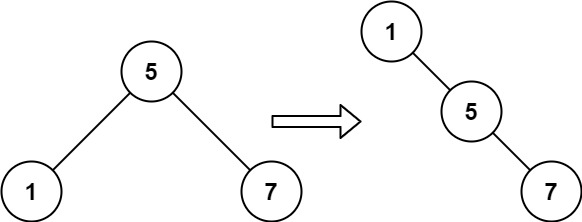
Input: root = [5,1,7]
Output: [1,null,5,null,7]

 

Constraints:

• The number of nodes in the given tree will be in the range [1, 100].
• 0 <= Node.val <= 1000

Solution(Python)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def increasingBST(self, root: TreeNode) -> TreeNode:
        return self.morrisTraversal(root)

    # Time Complexity: O(n)
    # Space Complexity: O(n)
    def recursiveInorderTraversal(self, root):
        def inorder(node):
            if node:
                yield from inorder(node.left)
                yield node.val
                yield from inorder(node.right)

        ans = cur = TreeNode(None)

        for v in inorder(root):
            cur.right = TreeNode(v)
            cur = cur.right
        return ans.right

    # Time Complexity: O(n)
    # Space Complexity: O(H)
    def relink(self, root):
        def inorder(node):
            if node:
                inorder(node.left)
                node.left = None
                self.cur.right = node
                self.cur = node
                inorder(node.right)

        ans = self.cur = TreeNode(None)
        inorder(root)
        return ans.right

    # Time Complexity: O(n)
    # Space Complexity: O(1)
    def morrisTraversal(self, root):
        dummy = TreeNode(0)
        node = dummy
        curr = root
        while curr:
            if not curr.left:
                node.right = TreeNode(curr.val)
                # print(curr.val)
                node = node.right
                curr = curr.right
            else:
                pre = curr.left
                while pre and pre.right and pre.right != curr:
                    pre = pre.right
                if not pre.right:
                    pre.right = curr
                    curr = curr.left
                else:
                    pre.right = None
                    node.right = TreeNode(curr.val)
                    # print(curr.val)
                    node = node.right
                    curr = curr.right
        return dummy.right