84-largest-rectangle-in-histogram

Try it on leetcode

Description

Given an array of integers heights representing the histogram's bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.

 

Example 1:

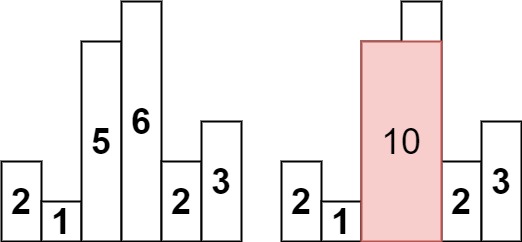
Input: heights = [2,1,5,6,2,3]
Output: 10
Explanation: The above is a histogram where width of each bar is 1.
The largest rectangle is shown in the red area, which has an area = 10 units.

Example 2:

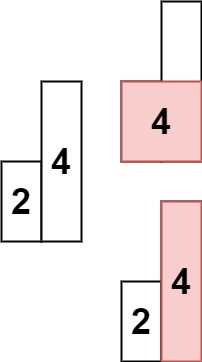
Input: heights = [2,4]
Output: 4

 

Constraints:

• 1 <= heights.length <= 105
• 0 <= heights[i] <= 104

Solution(Python)

class Solution:
    """
    for calculating a rectangle we need both width and height
    the width of the rectangle will be the difference of index positions
    and height will be the corresponding values

    Constraints:
        * 1 <= heights.length <= 10^5
        * 0 <= heights[i] <= 10^4

    1.Bruteforce:
        *we can start from every possible recatngles that can be formed from the given
         array
        *with respect to width we can make upto n^2 possible
        *while considering the height choose the rectangle with less height
      Implementation:
        maxRectangleArea
        for i in n:
            for j in n:
                maxRectangleArea = max(maxRectangleArea, (j-i+1) * min(arr[i],arr[j]) )
      Analysis:
        Time Complexity: O(n^2)
        Space Complexity: O(1)

    2. presum:
       Idea:
            bruteforcs can be written as

            for each index:
                maxarea = max(height[index]*(leftindex[i] - rightindex[i]))
            with precached the leftsmallest index and right smallest index
            we can optmize the bruteforce method

            for leftsmallest index move until we hit the smallest height
            similary for right smallest index repeat the process

       Analysis:
        Time Complexity: O(n)
        Space Complexity: O(n)

    3. stacks:
        in presum technique we only cache the information of bars in increaing heights

        instead of using two separate arrays to store it's value

        we can use a stack of bars we identified so far with only bars greater than current bar
      Analysis:
        Time Complexity: O(n)
        Space Complexity: O(n)

    """

    def largestRectangleArea(self, heights: List[int]) -> int:
        return self.stack(heights)

    def bruteforce(self, heights: List[int]) -> int:
        n = len(heights)
        maxRec = float("-INF")
        for i in range(n):
            curHeight = heights[i]
            for j in range(i, n):
                curHeight = min(curHeight, heights[j])
                maxRec = max(maxRec, abs(j - i + 1) * curHeight)

        return maxRec

    def presum(self, heights: List[int]) -> int:
        n = len(heights)

        left = [0] * n
        right = [0] * n

        left[0] = -1
        right[n - 1] = n

        for i in range(1, n):
            curr = i - 1
            while curr >= 0 and heights[i] <= heights[curr]:
                curr = left[curr]
            left[i] = curr

        for i in range(n - 2, -1, -1):
            curr = i + 1
            while curr <= n - 1 and heights[i] <= heights[curr]:
                curr = right[curr]
            right[i] = curr

        maxRec = float("-INF")
        for i in range(n):
            maxRec = max(maxRec, heights[i] * (right[i] - left[i] - 1))
        return maxRec

    def stack(self, heights: List[int]) -> int:
        heights.append(0)
        stack = []
        maxRec = 0
        n = len(heights)
        for i in range(n):
            height = heights[i]
            while stack and heights[stack[-1]] >= height:
                H = heights[stack.pop()]
                W = i if not stack else i - stack[-1] - 1
                maxRec = max(maxRec, H * W)
            stack.append(i)
        return maxRec